What Happens To Points At The Same Distance From Camera If The Scene Is A Tilted Plane

Tilt-lens photo of a model train. The lens was swung towards right, in guild to keep the plane of focus along the train. The sensor aeroplane, the lens plane and the plane along the railroad train all intersect to the right of the camera.

A scientific photographic camera with a Scheimpflug adaptor mounted between the lens and the camera, showing in cease-movement the potential movements the adaptor provides in the two axes (tilt and swing).

The Scheimpflug principle is a description of the geometric relationship between the orientation of the airplane of focus, the lens airplane, and the image plane of an optical system (such as a camera) when the lens plane is not parallel to the image aeroplane. It is applicable to the use of some camera movements on a view camera. It is also the principle used in corneal pachymetry, the mapping of corneal topography, done prior to refractive heart surgery such equally LASIK, and used for early detection of keratoconus. The principle is named after Austrian army Captain Theodor Scheimpflug, who used information technology in devising a systematic method and apparatus for correcting perspective distortion in aeriform photographs, although Helm Scheimpflug himself credits Jules Carpentier with the rule, thus making it an case of Stigler'southward law of eponymy.

Description [edit]

Figure 1. With a normal camera, when the subject is not parallel to the image airplane, only a small region is in focus.

Figure 2. The angles of the Scheimpflug principle, using the instance of a photographic lens

Effigy 3. Rotation of the aeroplane of focus

Effigy 4. Rotation-centrality distance and angle of the PoF

Commonly, the lens and paradigm (moving-picture show or sensor) planes of a camera are parallel, and the plane of focus (PoF) is parallel to the lens and epitome planes. If a planar subject (such as the side of a building) is also parallel to the image plane, it can coincide with the PoF, and the entire field of study can exist rendered sharply. If the field of study plane is not parallel to the image airplane, information technology volition be in focus only forth a line where information technology intersects the PoF, as illustrated in Figure 1.

Simply when a lens is tilted with respect to the paradigm aeroplane, an oblique tangent extended from the image plane and some other extended from the lens plane meet at a line through which the PoF also passes, every bit illustrated in Figure 2. With this condition, a planar subject field that is non parallel to the epitome plane can be completely in focus. While many photographers were/are unaware of the verbal geometric relationship between the PoF, lens airplane, and film aeroplane, swinging and tilting the lens to swing and tilt the PoF was practiced since the mid-1800s. But, when Carpentier and Scheimpflug wanted to produce equipment to automate the process, they needed to find a geometric relationship.

Scheimpflug (1904) referenced this concept in his British patent; Carpentier (1901) too described the concept in an earlier British patent for a perspective-correcting photographic enlarger. The concept can exist inferred from a theorem in projective geometry of Gérard Desargues; the principle likewise readily derives from simple geometric considerations and application of the Gaussian thin-lens formula, every bit shown in the section Proof of the Scheimpflug principle.

Changing the plane of focus [edit]

When the lens and image planes are not parallel, adjusting focus^[a] rotates the PoF rather than merely displacing information technology forth the lens axis. The centrality of rotation is the intersection of the lens's front focal plane and a plane through the center of the lens parallel to the epitome plane, as shown in Figure three. As the image plane is moved from IP₁ to IP₂, the PoF rotates well-nigh the axis One thousand from position PoF_i to position PoF₂; the "Scheimpflug line" moves from position S_ane to position S_two. The axis of rotation has been given many dissimilar names: "counter centrality" (Scheimpflug 1904), "hinge line" (Merklinger 1996), and "pivot bespeak" (Wheeler).

Refer to Figure 4; if a lens with focal length f is tilted by an angle θ relative to the paradigm plane, the altitude J ^[b] from the heart of the lens to the axis G is given past

${\displaystyle J={\frac {f}{\sin \theta }}.}$

If five′ is the distance forth the line of sight from the image plane to the center of the lens, the angle ψ between the image aeroplane and the PoF is given past^[c]

${\displaystyle \tan \psi ={\frac {v'}{v'\cos \theta -f}}\sin \theta .}$

Equivalently, on the object side of the lens, if u′ is the distance along the line of sight from the middle of the lens to the PoF, the angle ψ is given by

${\displaystyle \tan \psi ={\frac {u'}{f}}\sin \theta .}$

The angle ψ increases with focus distance; when the focus is at infinity, the PoF is perpendicular to the paradigm aeroplane for any nonzero value of tilt. The distances u′ and v′ forth the line of sight are not the object and image distances u and v used in the thin-lens formula

${\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {i}{f}},}$

where the distances are perpendicular to the lens plane. Distances u and v are related to the line-of-sight distances past u = u′ cosθ and v = five′ cosθ .

For an essentially planar subject, such as a roadway extending for miles from the camera on flat terrain, the tilt tin be set to identify the axis Thousand in the subject plane, and the focus then adjusted to rotate the PoF so that it coincides with the subject area plane. The entire field of study can be in focus, fifty-fifty if it is not parallel to the image aeroplane.

The plane of focus too can be rotated and so that it does non coincide with the subject plane, and and so that only a small function of the subject is in focus. This technique sometimes is referred to as "anti-Scheimpflug", though it actually relies on the Scheimpflug principle.

Rotation of the plane of focus can be accomplished by rotating either the lens plane or the image plane. Rotating the lens (as past adjusting the front end standard on a view camera) does not alter linear perspective^[d] in a planar subject field such as the face of a building, but requires a lens with a big image circle to avoid vignetting. Rotating the image airplane (as by adjusting the back or rear standard on a view camera) alters perspective (e.g., the sides of a building converge), but works with a lens that has a smaller prototype circle. Rotation of the lens or back about a horizontal axis is commonly called tilt, and rotation nigh a vertical centrality is commonly chosen swing.

Camera movements [edit]

Tilt and swing are movements available on most view cameras, oft on both the front and rear standards, and on some small- and medium format cameras using special lenses that partially emulate view-camera movements. Such lenses are often chosen tilt-shift or "perspective command" lenses.^[east] For some photographic camera models there are adapters that enable movements with some of the manufacturer'due south regular lenses, and a crude approximation may be achieved with such attachments every bit the 'Lensbaby' or past 'freelensing'.

Depth of field [edit]

Figure 5. Depth of field when the PoF is rotated

When the lens and image planes are parallel, the depth of field (DoF) extends between parallel planes on either side of the airplane of focus. When the Scheimpflug principle is employed, the DoF becomes wedge shaped (Merklinger 1996, 32; Tillmanns 1997, 71),^[f] with the apex of the wedge at the PoF rotation axis,^[k] as shown in Figure v. The DoF is zero at the apex, remains shallow at the edge of the lens's field of view, and increases with distance from the camera. The shallow DoF near the photographic camera requires the PoF to exist positioned carefully if near objects are to be rendered sharply.

On a airplane parallel to the image plane, the DoF is equally distributed to a higher place and below the PoF; in Figure 5, the distances y _n and y _f on the plane VP are equal. This distribution tin exist helpful in determining the best position for the PoF; if a scene includes a distant tall feature, the best fit of the DoF to the scene oftentimes results from having the PoF pass through the vertical midpoint of that feature. The angular DoF, withal, is not equally distributed well-nigh the PoF.

The distances y _n and y _f are given past (Merklinger 1996, 126)

${\displaystyle y_{x}={\frac {f}{v'}}{\frac {u'}{u}}_{\mathrm {h} }J\,,}$

where f is the lens focal length, five′ and u′ are the image and object distances parallel to the line of sight, u _h is the hyperfocal distance, and J is the altitude from the middle of the lens to the PoF rotation axis. By solving the paradigm-side equation for tan ψ for v′ and substituting for v′ and u _h in the equation higher up,^[h] the values may exist given equivalently by

${\displaystyle y_{x}={\frac {Nc}{f}}\left({\frac {ane}{\tan \theta }}-{\frac {i}{\tan \psi }}\right)u'\,,}$

where N is the lens f-number and c is the circumvolve of confusion. At a large focus distance (equivalent to a large angle between the PoF and the image plane), v′ ≈ f , and (Merklinger 1996, 48)^[i]

${\displaystyle y_{x}\approx {\frac {u'}{u}}_{\mathrm {h} }J\,,}$

or

${\displaystyle y_{x}\approx {\frac {Nc}{f}}{\frac {u'}{\tan \theta }}\,.}$

Thus at the hyperfocal distance, the DoF on a plane parallel to the image airplane extends a distance of J on either side of the PoF.

With some subjects, such as landscapes, the wedge-shaped DoF is a good fit to the scene, and satisfactory sharpness tin often exist achieved with a smaller lens f-number (larger aperture) than would be required if the PoF were parallel to the image plane.

Selective focus [edit]

James McArdle (1991) Accomplices.

The region of sharpness tin also be fabricated very small by using big tilt and a small f-number. For case, with eight° tilt on a 90 mm lens for a small-format photographic camera, the total vertical DoF at the hyperfocal distance is approximately^[j]

${\displaystyle 2J=2{\frac {f}{\sin \theta }}=2\times {\frac {xc{\text{ mm}}}{\sin viii^{\circ }}}=1293{\text{ mm}}\,.}$

At an discontinuity of f/2.viii, with a circle of confusion of 0.03 mm, this occurs at a altitude u′ of approximately

${\displaystyle {\frac {f^{2}}{Nc}}={\frac {90^{2}}{2.viii\times 0.03}}=96.4{\text{ m}}\,.}$

Of course, the tilt also affects the position of the PoF, so if the tilt is chosen to minimize the region of sharpness, the PoF cannot be fix to pass through more than one arbitrarily chosen point. If the PoF is to pass through more than 1 capricious betoken, the tilt and focus are fixed, and the lens f-number is the only available command for adjusting sharpness.

Derivation of the formulas [edit]

Proof of the Scheimpflug principle [edit]

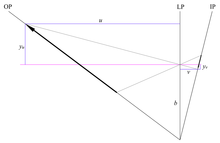
Figure 6. Object plane inclined to the lens plane

In a two-dimensional representation, an object plane inclined to the lens aeroplane is a line described past

${\displaystyle y_{u}=au+b}$ .

By optical convention, both object and image distances are positive for real images, so that in Figure 6, the object altitude u increases to the left of the lens airplane LP; the vertical centrality uses the normal Cartesian convention, with values in a higher place the optical axis positive and those below the optical axis negative.

The human relationship betwixt the object distance u, the image distance v, and the lens focal length f is given by the thin-lens equation

${\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}}\,;}$

solving for u gives

${\displaystyle u={\frac {vf}{v-f}}\,,}$

then that

${\displaystyle y_{u}=a\,{\frac {vf}{5-f}}+b}$ .

The magnification thou is the ratio of image summit y_v to object height y_u  :

${\displaystyle m={\frac {y_{v}}{y_{u}}}\,;}$

y_u and y_five are of reverse sense, so the magnification is negative, indicating an inverted image. From similar triangles in Effigy 6, the magnification as well relates the image and object distances, and so that

${\displaystyle 1000=-{\frac {v}{u}}=-{\frac {v-f}{f}}}$ .

On the image side of the lens,

${\displaystyle {\brainstorm{aligned}y_{5}&=my_{u}\\&=-{\frac {five-f}{f}}\left(a\,{\frac {vf}{v-f}}+b\right)\\&=-\left(av+{\frac {v}{f}}b-b\right)\,,\terminate{aligned}}}$

giving

${\displaystyle y_{5}=-\left(a+{\frac {b}{f}}\right)v+b}$ .

The locus of focus for the inclined object airplane is a airplane; in two-dimensional representation, the y-intercept is the same as that for the line describing the object plane, so the object plane, lens plane, and image airplane have a mutual intersection.

A similar proof is given by Larmore (1965, 171–173).

Bending of the PoF with the image plane [edit]

Figure vii. Angle of the PoF with the prototype aeroplane

From Figure 7,

${\displaystyle \tan \psi ={\frac {u'+5'}{S}}\,,}$

where u′ and five′ are the object and image distances along the line of sight and South is the distance from the line of sight to the Scheimpflug intersection at S. Again from Figure 7,

${\displaystyle \tan \theta ={\frac {v'}{S}}\,;}$

combining the previous 2 equations gives

${\displaystyle \tan \psi ={\frac {u'+v'}{five'}}\tan \theta =\left({\frac {u'}{v'}}+ane\right)\tan \theta \,.}$

From the sparse-lens equation,

${\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{u'\cos \theta }}+{\frac {1}{five'\cos \theta }}={\frac {1}{f}}\,.}$

Solving for u′ gives

${\displaystyle u'={\frac {five'f}{v'\cos \theta -f}}\,;}$

substituting this upshot into the equation for tanψ gives

${\displaystyle \tan \psi =\left({\frac {f}{five'\cos \theta -f}}+1\right)\tan \theta ={\frac {f+v'\cos \theta -f}{v'\cos \theta -f}}\tan \theta \,,}$

or

${\displaystyle \tan \psi ={\frac {v'}{five'\cos \theta -f}}\sin \theta \,.}$

Similarly, the thin-lens equation can be solved for v′, and the consequence substituted into the equation for tanψ to give the object-side relationship

${\displaystyle \tan \psi ={\frac {u'}{f}}\sin \theta \,.}$

Noting that

${\displaystyle {\frac {u'}{f}}={\frac {u}{f}}{\frac {1}{\cos \theta }}={\frac {m+i}{one thousand}}{\frac {1}{\cos \theta }}\,,}$

the human relationship between ψ and θ tin be expressed in terms of the magnification m of the object in the line of sight:

${\displaystyle \tan \psi ={\frac {m+one}{m}}\tan \theta \,.}$

Proof of the "swivel rule" [edit]

From Figure 7,

${\displaystyle \tan \psi ={\frac {u'}{J}}\,;}$

combining with the previous upshot for the object side and eliminating ψ gives

${\displaystyle \sin \theta ={\frac {f}{J}}\,.}$

Again from Figure 7,

${\displaystyle \sin \theta ={\frac {d}{J}}\,,}$

so the distance d is the lens focal length f, and the point One thousand is at the intersection the lens's front focal airplane with a line parallel to the image aeroplane. The distance J depends only on the lens tilt and the lens focal length; in particular, information technology is non affected by changes in focus. From Figure 7,

${\displaystyle \tan \theta ={\frac {v'}{South}}\,,}$

and so the distance to the Scheimpflug intersection at S varies as the focus is changed. Thus the PoF rotates about the axis at 1000 as focus is adjusted.

Notes [edit]

1. ^ Strictly, the PoF rotation axis remains fixed but when focus is adapted by moving the camera back, as on a view camera. When focusing past moving the lens, in that location is a slight motion of the rotation centrality, merely except for very small camera-to-subject distances, the motion is usually insignificant.
2. ^ The symbol J for the distance from the center of the lens to the PoF rotation axis was introduced by Merklinger (1996), and manifestly has no detail significance.
3. ^ Merklinger (1996, 24) gives the formula for the bending of the plane of focus as

   ${\displaystyle {\frac {v'}{f}}=\sin \theta \left[{\frac {1}{\tan \left(\psi -\theta \correct)}}+{\frac {one}{\tan \theta }}\correct]\,;}$

   by application of the angle-divergence formula for the tangent and rearrangement, it tin be transformed into the form given in this commodity.
4. ^ Strictly, keeping the prototype plane parallel to a planar subject maintains perspective in that subject only when the lens is of symmetrical blueprint, i.e., the entrance and exit pupils coincide with the nodal planes. About view-photographic camera lenses are nearly symmetrical, merely this is not e'er the case with tilt/shift lenses used on pocket-sized- and medium-format cameras, especially with wide-angle lenses of retrofocus design. If a retrofocus or telephoto lens is tilted, the bending of the camera back may need to exist adapted to maintain perspective.
5. ^ The primeval Nikon perspective-control lenses included simply shift, hence the designation "PC"; Nikon PC lenses introduced since 1999 also include tilt just retain the earlier designation.
6. ^ When the lens plane is not parallel to the image plane, the blur spots are ellipses rather than circles, and the limits of DoF are not exactly planar. In that location is picayune data on human being perception of elliptical rather than circular blurs, but taking the major axis of the ellipse as the governing dimension is arguably the worst-case condition. Using this supposition, Robert Wheeler examines the upshot of elliptical blur spots on DoF limits for a tilted lens in his Notes on View Camera Geometry; he concludes that in typical applications, the event is negligible, and that the assumption of planar DoF limits is reasonable. His analysis considers only points on a vertical airplane through the centre of the lens, however. Leonard Evens examines the effect of elliptical mistiness at any arbitrary bespeak in the epitome plane, and concludes that, in most cases, the error from assuming planar DoF limits is minor.
7. ^ Tillmanns indicates that this behavior was discovered during the evolution of the Sinar e camera (released in 1988), and that prior to that, the DoF wedge was thought to extend to the line of intersection of the object, lens, and image planes. He does not talk over the rotation of the PoF about the apex of the DoF wedge.
8. ^ Merklinger uses the approximation u _h ≈ f²/N c to derive his formula, so the substitution here is exact.
9. ^ Strictly, as the focus distance approaches infinity, 5′ cos θ → f ; hence, the guess formulas differ by a factor of cos θ . At small values of θ, cos θ ≈ 1, so the difference is negligible. With large values of tilt, as occasionally might be needed with a large-format camera, the fault becomes greater, and either the exact formula or the estimate formula in terms of tan θ should be used.
10. ^ The example here uses Merklinger's approximation. For modest values of tilt, sinθ ≈ tanθ , so the error is minimal; for large values of tilt, the denominator should be tanθ .

References [edit]

• Carpentier, Jules. 1901. Improvements in Enlarging or like Cameras. GB Patent No. 1139. Filed 17 January 1901, and issued 2 Nov 1901. Available for download (PDF).
• Larmore, Lewis. 1965. Introduction to Photographic Principles. New York: Dover Publications, Inc.
• Merklinger, Harold M. 1996. Focusing the View Camera. Bedford, Nova Scotia: Seaboard Printing Limited. ISBN 0-9695025-ii-4. Available for download (PDF).
• Scheimpflug, Theodor. 1904. Improved Method and Appliance for the Systematic Amending or Distortion of Airplane Pictures and Images by Means of Lenses and Mirrors for Photography and for other purposes. GB Patent No. 1196. Filed 16 January 1904, and issued 12 May 1904. Available for download (PDF).
• Tillmanns, Urs. 1997. Creative Large Format: Basics and Applications. second ed. Feuerthalen, Switzerland: Sinar AG. ISBN three-7231-0030-9
• Steger, Carsten (2017). "A Comprehensive and Versatile Photographic camera Model for Cameras with Tilt Lenses". International Journal of Computer Vision. 123: 121–159. doi:10.1007/s11263-016-0964-8.

External links [edit]

• View Camera Geometry (PDF) by Leonard Evens. Analysis of the issue of elliptical blur spots on DoF
• Depth of Field for the Tilted Lens (PDF) by Leonard Evens. A more applied and more than accessible summary of View Camera Geometry
• How to Focus the View Camera by Quang-Tuan Luong. Includes discussion of how to gear up the airplane of focus
• The Scheimpflug Principle past Harold Merklinger
• Addendum to Focusing the View Camera (PDF) by Harold Merklinger
• Unilateral Real-time Scheimpflug Videography to Study Accommodation Dynamics in Homo Optics (PDF) by Ram Subramanian
• Notes on View Camera Geometry (PDF) past Robert Wheeler
• Tilt and Shift Lenses: Tailored towards small-format tilt-shift lenses, just principles apply to any format

Source: https://en.wikipedia.org/wiki/Scheimpflug_principle

Posted by: weinmanndraugh.blogspot.com

Share this post